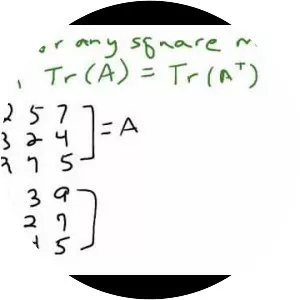
Trace
In linear algebra, the trace of a square matrix A is defined to be the sum of elements on the main diagonal of A. The "trace" of a matrix is sum of the eigenvalues, and it is invariant with respect to a change of basis. This characterization can be used to define the "trace" of a linear operator in general.




